Chapter 8 (Gravity)

Gravity

Gravity on a small scale:

 

Attractive Force (Newton’s Law):                      

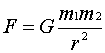                                              Where:            m1 and m2 are small masses; r is the separation G is the Gravitiational constant = 6.672 x 10-8 m3/mg.s2

 

 

Gravity on Earth

The calculation is based on point masses, therefore assuming the earth has concentric layers we can say me is the center and ms is at its surface separated by Re and can use Newtons law:                    

 

 

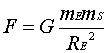
In terms of acceleration this equation becomes:      

                                                                                              

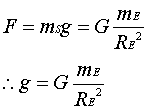
Where:            g = accelaeration due to gravity

Mass of the earth

Using equation 8.4 we can calculate the mass of the earth:

Ø      We have found that the average mass is 5.5 Mg/m3

Ø      Because rock at the surface are much less (generally < 3.0 Mg/m3) we know the center of earth is more dense

Densities of Rocks: Rock densities are typically less at the surface than at depth. This is due to weathering and fracturing.

Units of density:

Ø       Mg/m3

Ø      g/cc, which compares to the density of water (~1) 

Ø       kg/m3, which is 1000x larger

Gravity units:

Given the example in the book (Eq. 8.5):

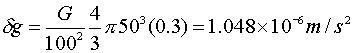
These units are too small so we use mGal instead:

where: 

 

 

Gravity anomalies of some bodies

Calculating gravity anomalies:

Calculated using vectors summed as per the pull on the mass to the surrounding area (measuring the excess).

Sphere and Cylinder:

Ø      At depth there will be no sharp edges

Ø      The anomaly will be more defined the closer to the surface it is

Sheets:

Sheetlike bodies include dikes, sills (slab) or veins; again more definition, the shallower the feature.

If a slab produces no anomaly, it’s excess density will increase “g” by an amount that can be calculated by:

where: t is the thickness of the slab

Calculations are usually accomplished by breaking shapes into smaller sections.  This allows us to model the anomaly more easily.

Measuring Gravity:

The Gravimeter

3 ways  to do this:

1)     Measure the time it takes for an object to fall

2)     Use a pendulum

3)     Use a spring balance

Modern meters can measure changes in “g” as small as a hundredth of mGal or 10-8g.

Data Reduction:

–        Measuring lateral variations of “g”

–        Always start at a base station where the value of “g” is known

–        Conversion of the readings depends on the meter

Types of conversions:

Drift: caused by slow creep of the spring and tidal variations, which can be up to 0.3mGal in a day.  Drift is measured by returning to the base station throughout the day.

Latitude: equatorial bulge created by the rotation of the earth

–        We can correct for latitude effects by using the International Gravity Formula

 

–        For a surveyor that is <10's of km variations can be proportional to the distance:

 polewards; where l is the latitude where the survey is being made

Eötvös correction: typically associated with shipborne or airborne surveys

; where v is the speed (kph), l is the latitude and a is the direction of travel (measured clockwise)

Topography correction:

1)     Free-air correction: need for position in spave of the gravimeter (affected by a rise in cm’s)

2)     Bouguer correction: corrects for pull of rock bodies in the surrounding area

–        Because both Free-air and Bouguer corrections are dependent on “h” the equations can be combined:

3)     Terrain correction: This takes into account the changing topography in a survey area

–        Once all the corrections are made the anomaly is called a Bouguer Anomoly

Bouguer Anomoly = observed “g” + free-air correction – Bouguer correction + terrain correction – latitude correction + Eötvös correction

Simple Bouguer: lacks terrain correction (if very small)

* Purpose: to produce a value of “g” without the effects of topography and latitude

Residual and regional anomalies: at depth we try to separate anomalies.  This is done so that we can discern different features.  The residual anomaly is subtracted from the total anomaly.  Like in the example for the book, subtractins out the residual for the regional, the residual is the dike.  The regional is the granite and surrounding rocks.

 

 

Surveys

Planning a survey

1)     want to define a target

2)     Need to determine the precision (e.g., 10mGal anomaly need precision to 1mGal and heights need to be known to about 30 cm)

3)     The survey should be longer than the feature

4)     To increase accuracy you need to visit a base station often

5)     Ideally we would like to get an in situ measurement of density.  Alternatively, we can use Garnders Rule for estimating velocity to density

Marine surveys:

–        Average readings over time

–         Eötvös correction

–        Usually these surveys are no better than 1mGal (this can be obtained with Satellite gravity surveys)

–        In deep water (no Bouguer correction); resulting anomaly is a “free-air anomaly”

Airborne surveys:

–        Accuracy is 5 to 20 mGal

–        Good for areas with access issues

 

 

Modelling and Inversion

*Gravity models are commonly non-unique solutions (you can come up with a variety of models for the same data).

*Because we are measuring density contrasts it is essential to use the known geology as a starting or reference for density modeling.

Depth rules:

The sharpness of a measurement or gradient tells you that there is the boundary of an object.  This sharpness is measured as half width.  Fig 8.19 in your text gives you some rule for half-width calculations.  If the shape is unknown, the steepest slope is used and the total height of the anomaly.  When modeling, the bodies are defined as polygons with uniform densities.

Total excess mass:

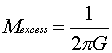    (Volume of the anomaly); or you can use: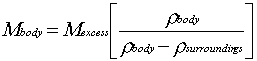       

Microgravity:

Ø      Used to target anomalies of <0.1 mGal

Ø      Typically used for environmental or civil engineering projects

Ø      Can look for gaps or holes (caves)